Hàm hợp đạo hàm: Cách sử dụng và tính toán – Bấm vào đây!

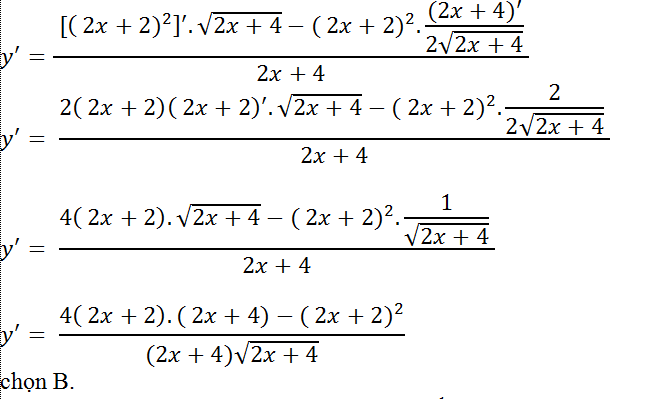
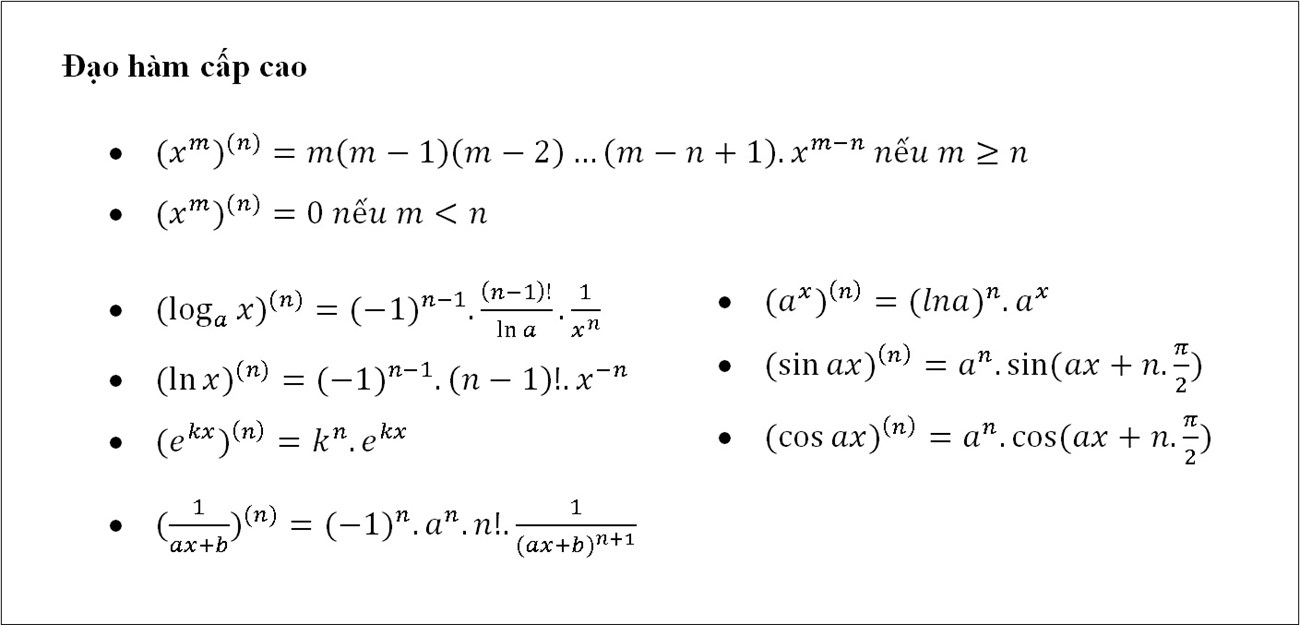
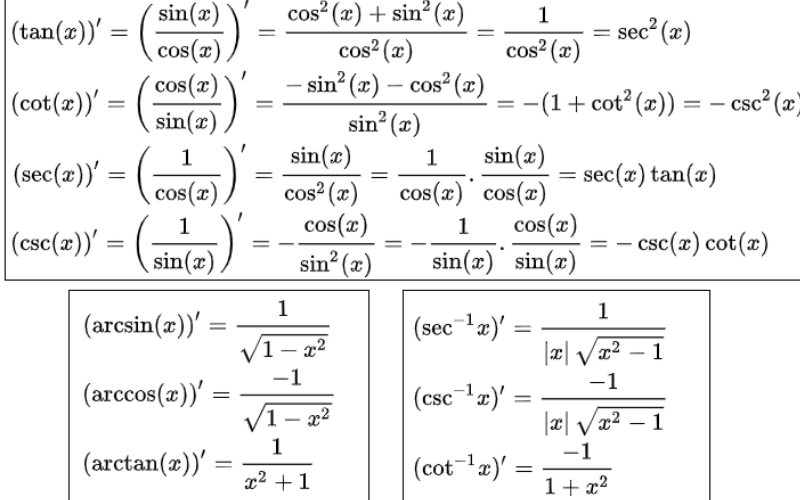
Hàm hợp đạo hàm là một khái niệm quan trọng trong toán học, đặc biệt là trong giải tích vi phân. Chúng ta sẽ đi sâu vào các khái niệm cơ bản của hàm hợp đạo hàm, ứng dụng của nó, và các đạo hàm riêng và cấp cao của hàm hợp đạo hàm.

Các khái niệm cơ bản về hàm hợp đạo hàm

Định nghĩa hàm hợp đạo hàm

Hàm hợp đạo hàm là một hàm số được xác định bởi công thức sau: f(g(x)) với f(x) và g(x) đều là hàm số. Đánh giá f(g(x)) tại x = a bằng cách đưa giá trị x = a vào g(x) để tính ra giá trị của g(a), sau đó đưa giá trị đó vào hàm số f(x) để tính ra giá trị f(g(a)).

Công thức tính toán hàm hợp đạo hàm

Đạo hàm của hàm hợp đạo hàm được tính bằng cách sử dụng quy tắc chuỗi như sau: f'(g(x))g'(x), trong đó f'(x) là đạo hàm của hàm số f(x) và g'(x) là đạo hàm của hàm số g(x).

Ví dụ minh họa về hàm hợp đạo hàm

Giả sử ta có các hàm số f(x) = x^2 và g(x) = 2x + 1. Ta muốn tính đạo hàm của hàm hợp đạo hàm f(g(x)). Đầu tiên, ta tính g'(x) bằng cách lấy đạo hàm của hàm số g(x): g'(x) = d(2x + 1)/dx = 2. Tiếp theo, ta tính f'(g(x)) bằng cách lấy đạo hàm của hàm số f(x) tại x = g(x): f'(g(x)) = d(x^2)/dx = 2x. Gộp hai kết quả lại, ta có đạo hàm của hàm hợp đạo hàm f(g(x)): f'(g(x))g'(x) = 2x * 2 = 4x.

Ứng dụng của hàm hợp đạo hàm

Giải phương trình vi phân

Hàm hợp đạo hàm có thể được sử dụng để giải các phương trình vi phân phức tạp, bao gồm việc tính đạo hàm của một hàm số theo biến động của một hàm số khác. Điều này giúp ta có thể tính được các giá trị xấp xỉ của nghiệm của phương trình vi phân mà không cần phải tìm chính xác từng giá trị.

Tính tốc độ, gia tốc và mô-men động học

Hàm hợp đạo hàm cũng được sử dụng để tính toán tốc độ, gia tốc và mô-men động học trong vật lý. Việc tính toán này giúp ta có thể hiểu rõ hơn về các quá trình di chuyển và chuyển động của các đối tượng trong không gian.

Thuật toán tính số gần đúng cho hàm một biến

Hàm hợp đạo hàm cũng có thể được sử dụng để tính toán số gần đúng cho hàm số một biến. Việc này đóng vai trò quan trọng trong việc tính toán các vấn đề toán học phức tạp, bao gồm giải phương trình hoặc tính toán tích phân.

Đạo hàm riêng của hàm hợp đạo hàm

Định nghĩa và công thức tính đạo hàm riêng

Đạo hàm riêng của hàm hợp đạo hàm là đạo hàm của hàm số theo một biến cụ thể. Để tính đạo hàm riêng của hàm hợp đạo hàm, ta sử dụng quy tắc chuỗi như sau: d[f(g(x))]/dx = f'(g(x)) * g'(x).

Mối quan hệ giữa đạo hàm riêng và hàm hợp đạo hàm

Đạo hàm riêng của hàm hợp đạo hàm phụ thuộc vào hàm số g(x). Nếu ta biến đổi hàm g(x), đạo hàm của hàm hợp đạo hàm sẽ thay đổi tương ứng.

Ví dụ minh họa

Giả sử ta có các hàm số f(x) = x^2 và g(x) = 2x + 1. Ta muốn tính đạo hàm riêng của hàm hợp đạo hàm f(g(x)) theo x. Theo công thức, ta có: d[f(g(x))]/dx = f'(g(x)) * g'(x) = 2x * 2 = 4x.

Đạo hàm cấp cao của hàm hợp đạo hàm

Định nghĩa và công thức tính đạo hàm cấp cao

Đạo hàm cấp cao của hàm hợp đạo hàm là đạo hàm của hàm số theo một biến cụ thể, được tính bằng cách lấy đạo hàm của đạo hàm riêng của hàm hợp đạo hàm theo biến đó. Công thức tính đạo hàm cấp cao của hàm hợp đạo hàm là: d^nf(g(x))/dx^n = d^(n-1)[f'(g(x))g'(x)]/dx^(n-1).

Ứng dụng của đạo hàm cấp cao

Đạo hàm cấp cao của hàm hợp đạo hàm có thể được sử dụng trong việc giải các phương trình vi phân phức tạp, tính toán tốc độ và gia tốc của các đối tượng trong không gian, và tính toán số gần đúng cho các hàm số phức tạp.

Ví dụ minh họa về đạo hàm cấp cao của hàm hợp đạo hàm

Giả sử ta có các hàm số f(x) = x^4 và g(x) = 2x + 1. Ta muốn tính đạo hàm cấp cao thứ 3 của hàm hợp đạo hàm f(g(x)) theo x. Đầu tiên, ta tính đạo hàm riêng theo x: d[f(g(x))]/dx = 4x^3 * 2 = 8x^3. Tiếp theo, ta tính đạo hàm cấp hai: d^2[f(g(x))]/dx^2 = d/dx[8x^3] = 24x^2. Cuối cùng, ta tính đạo hàm cấp ba: d^3[f(g(x))]/dx^3 = d/dx[24x^2] = 48x.