Hoe Bereken Je De Stelling Van Pythagoras: Een Eenvoudige Uitleg

Pythagoras – Rechthoekszijden Berekenen – Wiskundeacademie

Keywords searched by users: hoe bereken je de stelling van pythagoras stelling van pythagoras formule, omgekeerde stelling van pythagoras, stelling van pythagoras berekenen, stelling van pythagoras calculator, stelling van pythagoras hoek berekenen, stelling van pythagoras in woorden, stelling van pythagoras oefeningen, stelling van pythagoras hoek berekenen online

Wat is de Stelling van Pythagoras?

De Stelling van Pythagoras is een belangrijk concept in de meetkunde dat de relatie tussen de zijden van een rechthoekige driehoek beschrijft. Deze stelling stelt dat in een rechthoekige driehoek, het kwadraat van de lengte van de schuine zijde gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden. Het wordt vaak gebruikt om de lengte van een zijde van een driehoek te berekenen wanneer de lengtes van de andere twee zijden bekend zijn.

De formule van de Stelling van Pythagoras

De formule van de Stelling van Pythagoras luidt als volgt: a² + b² = c². Hierbij staat a voor de lengte van de eerste zijde, b voor de lengte van de tweede zijde en c voor de lengte van de schuine zijde (hypotenusa) van de driehoek. Deze formule kan worden gebruikt om de lengte van elke zijde van een rechthoekige driehoek te berekenen als de lengtes van de andere twee zijden bekend zijn.

Hoe gebruik je de Stelling van Pythagoras?

Om de Stelling van Pythagoras toe te passen, moet u ervoor zorgen dat u over de juiste waarden beschikt. U moet de lengtes van twee zijden van de driehoek kennen voordat u de lengte van de derde zijde kunt berekenen. Hier zijn de stappen die u kunt volgen om de Stelling van Pythagoras toe te passen:

1. Identificeer de zijden van de driehoek: Wijs de zijde waarvan de lengte u wilt berekenen toe als “c” en de andere twee zijden als “a” en “b”.

2. Vierkant de lengtes: Neem de lengtes van de zijden a en b en kwadrateer ze door ze met zichzelf te vermenigvuldigen.

3. Tel de gekwadrateerde lengtes op: Tel de gekwadrateerde lengtes van zijde a en zijde b bij elkaar op.

4. Neem de vierkantswortel: Trek de vierkantswortel van het totaal van stap 3 om de waarde van zijde c te vinden.

Voorbeelden van berekeningen met de Stelling van Pythagoras

Om de formule en het gebruik van de Stelling van Pythagoras beter te begrijpen, laten we een paar voorbeelden bekijken:

Voorbeeld 1:
Stel dat zijde a van een rechthoekige driehoek een lengte heeft van 3 cm en zijde b een lengte heeft van 4 cm. We willen de lengte van zijde c berekenen.

a = 3 cm
b = 4 cm

Gebruik de formule van de Stelling van Pythagoras: a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²

Om c te vinden, nemen we de vierkantswortel van 25:
c = √25 = 5 cm

Dus de lengte van zijde c is 5 cm.

Voorbeeld 2:
Laten we zeggen dat zijde b van een rechthoekige driehoek een lengte heeft van 8 cm en zijde c een lengte heeft van 10 cm. We willen de lengte van zijde a berekenen.

b = 8 cm
c = 10 cm

Gebruik opnieuw de formule van de Stelling van Pythagoras: a² + b² = c²
a² + 8² = 10²
a² + 64 = 100
a² = 36

Om a te vinden, nemen we de vierkantswortel van 36:
a = √36 = 6 cm

Dus de lengte van zijde a is 6 cm.

Uitleg van de omgekeerde Stelling van Pythagoras

De omgekeerde Stelling van Pythagoras stelt dat als de som van de kwadraten van de lengtes van twee zijden van een driehoek gelijk is aan het kwadraat van de lengte van de derde zijde, de driehoek een rechthoekige driehoek is. Met andere woorden, als a² + b² = c², dan is de driehoek rechthoekig.

Praktisch gebruik van de Stelling van Pythagoras: de bouwhaak

Een praktisch gebruik van de Stelling van Pythagoras is te vinden in de bouw, waar een instrument genaamd een bouwhaak wordt gebruikt. Een bouwhaak is een driehoekig gereedschap dat wordt gebruikt om hoeken van 90 graden te controleren en te markeren. Het is gebaseerd op de Stelling van Pythagoras.

De zijden van een bouwhaak hebben een verhouding van 3:4:5. Dit betekent dat als de twee kortste zijden van een bouwhaak lengtes hebben van 3 en 4 eenheden, de langste zijde een lengte van 5 eenheden zal hebben. Dit is een direct gevolg van de Stelling van Pythagoras, waarbij 3² + 4² = 5².

De bouwhaak kan worden gebruikt om nauwkeurige haakse hoeken te construeren bij het bouwen van structuren, zoals muren, frames, en meubels.

FAQs:
1. Wat is de formule van de Stelling van Pythagoras?
De formule van de Stelling van Pythagoras is a² + b² = c², waarbij a en b de lengtes zijn van de twee rechthoekszijden en c de lengte is van de schuine zijde (hypotenusa) van de driehoek.

2. Hoe kan ik de Stelling van Pythagoras gebruiken?
Om de Stelling van Pythagoras te gebruiken, moet je de lengtes kennen van twee zijden van een rechthoekige driehoek. Met behulp van de formule a² + b² = c² kun je de lengte van de derde zijde berekenen.

3. Wat is de omgekeerde Stelling van Pythagoras?
De omgekeerde Stelling van Pythagoras stelt dat als de som van de kwadraten van de lengtes van twee zijden van een driehoek gelijk is aan het kwadraat van de lengte van de derde zijde, de driehoek rechthoekig is.

4. Wat is een bouwhaak en hoe wordt het gebruikt?
Een bouwhaak is een driehoekig gereedschap dat wordt gebruikt in de bouw om hoeken van 90 graden te controleren en te markeren. Het is gebaseerd op de Stelling van Pythagoras en heeft zijden in de verhouding 3:4:5. Het kan worden gebruikt om nauwkeurige haakse hoeken te construeren bij het bouwen van structuren.

Categories: Gevonden 47 Hoe Bereken Je De Stelling Van Pythagoras

Pythagoras - rechthoekszijden berekenen - WiskundeAcademie — Pythagoras – rechthoekszijden berekenen – WiskundeAcademie

De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a² + b² = c². Hierin zijn a en b de rechthoekszijden en c de schuine zijde.Euclides bewees de stelling van Pythagoras wel op een andere manier, door te stellen dat elk van de kleinere vierkanten gelijk is aan een rechthoekig deel van het grotere vierkant en de som van die twee rechthoekige delen precies het grote vierkant is.Rechte hoek aantonen

Als je alle zijden van de driehoek weet, maar je weet niet of een hoek 90 graden is, dan kan je dat controleren door te kijken of de stelling van Pythagoras geldt. Als het klopt dat a² + b² = c², dan heb je aangetoond dat de hoek inderdaad 90 graden is.

Vuistregels

Je kunt de Stelling van Pythagoras toepassen in rechthoekige driehoeken.
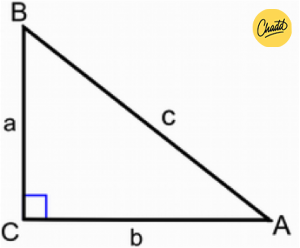
Stelling van Pythagoras: (ene rechthoekszijde)² + (andere rechthoekszijde)² = (schuine zijde)²
Of ook wel bekend als: a² + b² = c², waarbij a en b de rechthoekszijden zijn en c de schuine zijde is.

Hoe Bereken Je Pythagoras Uit?

Om Pythagoras te berekenen, kun je de Stelling van Pythagoras toepassen in rechthoekige driehoeken. Deze stelling zegt dat in een rechthoekige driehoek het kwadraat van de ene rechthoekszijde plus het kwadraat van de andere rechthoekszijde gelijk is aan het kwadraat van de schuine zijde. Dit kan ook worden geschreven als a2 + b2 = c2, waarbij a en b de lengtes van de rechthoekszijden zijn en c de lengte van de schuine zijde is.

Wie Bewees Stelling Van Pythagoras?

Euclides bewees de stelling van Pythagoras op een andere manier. Hij stelde dat elk van de kleinere vierkanten gelijk is aan een rechthoekig deel van het grotere vierkant. De som van deze twee rechthoekige delen is precies gelijk aan het grote vierkant. Deze bewijsmethode werd voor het eerst gepubliceerd in het jaar 300 voor Christus.

Hoe Bereken Je Een Hoek Van 90 Graden?

Hoe bereken je een hoek van 90 graden?

Om een hoek van 90 graden te berekenen, moet je kijken of de stelling van Pythagoras geldt. Als je alle zijden van de driehoek kent, maar niet zeker weet of een hoek 90 graden is, kun je dit controleren. Om de hoek te bevestigen, moet je controleren of a² + b² = c². Als deze vergelijking waar is, dan heb je aangetoond dat de hoek inderdaad 90 graden is. Dit is een belangrijke stap bij het berekenen van een rechte hoek.

Wat Is De Formule Van De Omgekeerde Stelling Van Pythagoras?

De omgekeerde stelling van Pythagoras werkt als volgt: in een rechthoekige driehoek geldt dat a^2 + b^2 = c^2. Met behulp van deze stelling kan men ook controleren of een driehoek waarvan alle drie de zijden bekend zijn, een rechthoekige driehoek is.

Wat Is Een 3 4 5 Driehoek?

Wat is een 3 4 5 driehoek? Een 3-4-5 driehoek is oorspronkelijk een bouwhaak. Een bouwhaak is een rechthoekige driehoek waarvan de lengtes van de rechthoekszijden 3 en 4 eenheden zijn, en de lengte van de tegenoverliggende zijde 5 eenheden is. Dit wordt ook wel de 3-4-5-stelling genoemd.

Aggregeren 44 hoe bereken je de stelling van pythagoras